第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
论文研究-自由空间损耗周期结构贴片/孔径电磁散射分析 .pdf
1．引言
2．目标的电磁建模和频域矩量法求解
3．数值算例
3.1 正方形贴片算例
3.2 矩形贴片算例
3.3 周期结构十字形孔径的电磁散射分析
4．结论
自由空间损耗周期结构贴片/孔径电磁散射分析
http://www.paper.edu.cn
电子科技大学电子薄膜与集成器件国家重点实验室，四川成都 (610054)
E-mail：tomclus006@163.com
孟 林
摘 要 ：本文采用频域矩量法对自由空间损耗周期结构贴片或孔径的电磁散射进行分析。计
算任意平面波入射下周期结构贴片/孔径元胞的表面等效感应电流分布和反射系数，把数值
结果与相关文献对比并对其进行讨论。
关键词：损耗周期结构，电磁散射，频域矩量法，表面等效感应电流，反射系数
1．引言
周期结构是二维周期性导体贴片或孔径元胞阵列，具有带阻或带通的滤波特性，在天线
罩、天线及光束调控系统，以及电磁兼容工程中都有广泛应用。周期结构可以制作成频率选
择表面[1]（Frequency Selective Surface），光子带隙（Photonic Bandgap）材料或电磁带隙
（ Electromagnetic Bandgap ） 材 料 [2] ， 以 及 具 有 负 介 电 常 数 和 负 磁 导 率 的 左 手 材 料
（Matamaterials）[3]。近年来有人把周期结构用于吸波材料以获得良好的性能，其中电子科
技大学的陈良等人把传统频率选择表面的导体贴片用电阻贴片代替，加不同厚度的介质基片
后制备出宽频吸波材料[4]。南京大学刘红英等人研究了FSS加载纳米吸波涂层涂敷金属板对
吸波材料在S波段性能的改善[5]。
对于周期结构的分析一般采用电磁场数值方法，如矩量法(MoM)，有限元法（FEM），
时域有限差分法（FDTD）等。东南大学的陆卫兵[6]提出一种有效的子域全域基函数，利用
矩量法对大尺寸有限单元的周期结构的电磁散射进行了精确分析。周永江[7]采用有限元法对
十字型频域选择表面进行了分析。马嘉俊[8]利用时域有限差分法对介质频率选择表面进行了
分析。本文基于Mittra[9]的频域矩量法对自由空间损耗周期结构贴片/孔径的电磁散射进行数
值分析,并与Barry[10]的矩量法结果进行对比，二者吻合的很好。
2．目标的电磁建模和频域矩量法求解
为了方便数值计算，首先我们做以下假设：a.整个周期结构具有无限大的尺寸，从而忽
略有限边界所带来的衍射效应；b.入射波为单色平面波；c.贴片屏的厚度很薄，忽略其厚度
做二维平面处理。
解决周期结构电磁波散射问题的第一步就是建立散射电场与周期结构元胞表面的感应
电流的关系，贴片表面感应电流是由于入射场引起的。首先让我们来考虑一个处于自由空间
的理想导体周期贴片问题，贴片处于 xy 二维平面，如图 1 所示矩形形周期结构贴片。
一个处于自由空间 xy 平面的导体贴片在平面波激励下的散射电场可以通过贴片表面感
应电流来计算。我们定义 J 为贴片表面的感应电流密度，A 为基于此电流的磁矢量位函数，
r 为场点，r’为源点，假定省略时间因子 exp(jωt),根据经典电磁理论我们可以得到源点 r’在
场点 r 处产生的散射场：
s
E
= −
j
ωμ
0
A
+
1
j
ωε
0
∇ ∇ ⋅
(
)A (1)
其中，
-1-
http://www.paper.edu.cn
Ei
z
Hi
ki
周期元胞
y
θ
a
φ
2a
x
b
2b
图 1 平面波入射周期元胞贴片示意图
A r
( )
=
G
∗
J
(2)
(3)
|
，星号表示卷积算子，G表示自由空间的格林函数。在导
G
= ∫
r r
G
( ,
r
r r J r
d
( ,
)
) (
′
′
′
jke
r r
0|
|
′
−
−
r r
4 |
′−
π
)
′ =
=
0ω με
k
k0是自由空间波数 0
体贴片上切相分量电场为零，用下标t来表示：
=
E E E
=
+
0
inc
t
s
t
上标 s 和 inc 分别对应于散射场和入射场。这样就可以把放出(1)式改写为
t
(4)
0
E r
( )
inc
t
= −
j
ωμ
0
A r
( )
t
−
∇ ∇ ⋅
(
⎡
⎣
A r
( )
)
⎤
⎦
t
(5)
1
j
ωε
0
(5)式就是针对理想导电贴片（Perfect Electric Conducting）的电场积分方程（Electric-field
integral equation）。对于厚度无限薄的屏，只存在x和y方向上的表面电流Jx，Jy，因此磁矢量
位函数只有Ax和Ay是非零的。这样我就可以得到(5)的矩阵形式：
−
E
E
inc
x
inc
y
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
−
=
j
ωμ
0
k
2
0
A G J
= ∗ ，
。
其中 x
对上式进行傅立叶变化，得到
A G J
= ∗
y
y
x
k
⎡
⎢
⎢
⎢
⎢
⎢
⎣
2
2
0
+
2
∂
x
∂
2
∂
x y
∂ ∂
2
∂
x y
∂ ∂
2
∂
y
∂
+
2
k
2
0
⎤
⎥
⎡
⎥ ⎢
⎥
⎣
⎥
⎥
⎦
A
x
A
y
⎤
⎥
⎦
(6)
−
E
E
inc
x
inc
y
⎡
⎢
⎢
⎣
x y
( ,
x y
( ,
)
)
⎤
⎥
⎥
⎦
=
1
2
π
∫
∞
∞
−∞ −∞
∫
k
−
2
1
α
j
ωε αβ
2
0
−
⎡
⎢
⎣
0
αβ
−
2
2
−
β
0
k
⎤
G
⎥
⎦
J
J
x
y
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
e
j x
j y
α β
e
d d
α β
(7)
考虑到贴片或孔径的空间周期性，利用 Floquet 定理，可以把 x 方向的电流展开为 Floquet
模式求和的形式
( )
J x
∞
= ∑
J e
m
m
=−∞
j m a k
(2
+
/
π
inc
x
)
x
(8)
其中 a 为周期元胞沿 x 方向的长度。我们对 y 方向的电流做同样的处理，可以把(7)式改写
为
-2-
−
⎡
⎢
⎢
⎣
E x y
( , )
inc
x
E x y
( , )
inc
y
⎤
⎥
⎥
⎦
=
2
π
j
ab
ωε
0
∞
∞
∑ ∑
=−∞ =−∞
n
m
http://www.paper.edu.cn
k
2
2
α αβ
−
m n
m
0
2
αβ
β
−
−
m n
n
−
k
2
0
⎡
⎢
⎣
⎤
G
⎥
⎦
(
α β
n
,
m
)
J
J
x
y
⎡
⎢
⎢
⎣
m
(
α β
n
(
α β
n
,
,
m
e
)
)
⎤
⎥
⎥
⎦
x
eα β
j
j
m
n
y
(9)
这样就把得积分方程中的连续卷积变为对无限个 Floquet 模式求和，每个求和项都是频域格
林函数与频域表面等效感应电流的内积。
本文选取屋顶基函数和刀片检验函数，利用矩量法把(9)式化为矩阵方程，求解出未知
电流系数后，可以得到表面等效感应电流分布，进而可以求得远场的反射系数。
3．数值算例
3.1 正方形贴片算例
我们对一个正方形金属贴片进行了分析，即取 Zs＝0。外加激励是垂直入射的 TM 平面
波，电场沿 x 方向极化，幅值为 E=120πV/cm。正方形的形状如图 1 所示,周期元胞的长宽均
为 0.3λ
，正方形贴片的长宽均为
0.15λ。
按照我们的前面的流程进行编程计算，我们只需画出一个周期元胞中的贴片上的电流大
小，这里我们把一个贴片离散成为 8×8 的网格，按编号调入电流基函数的参量，计算出来
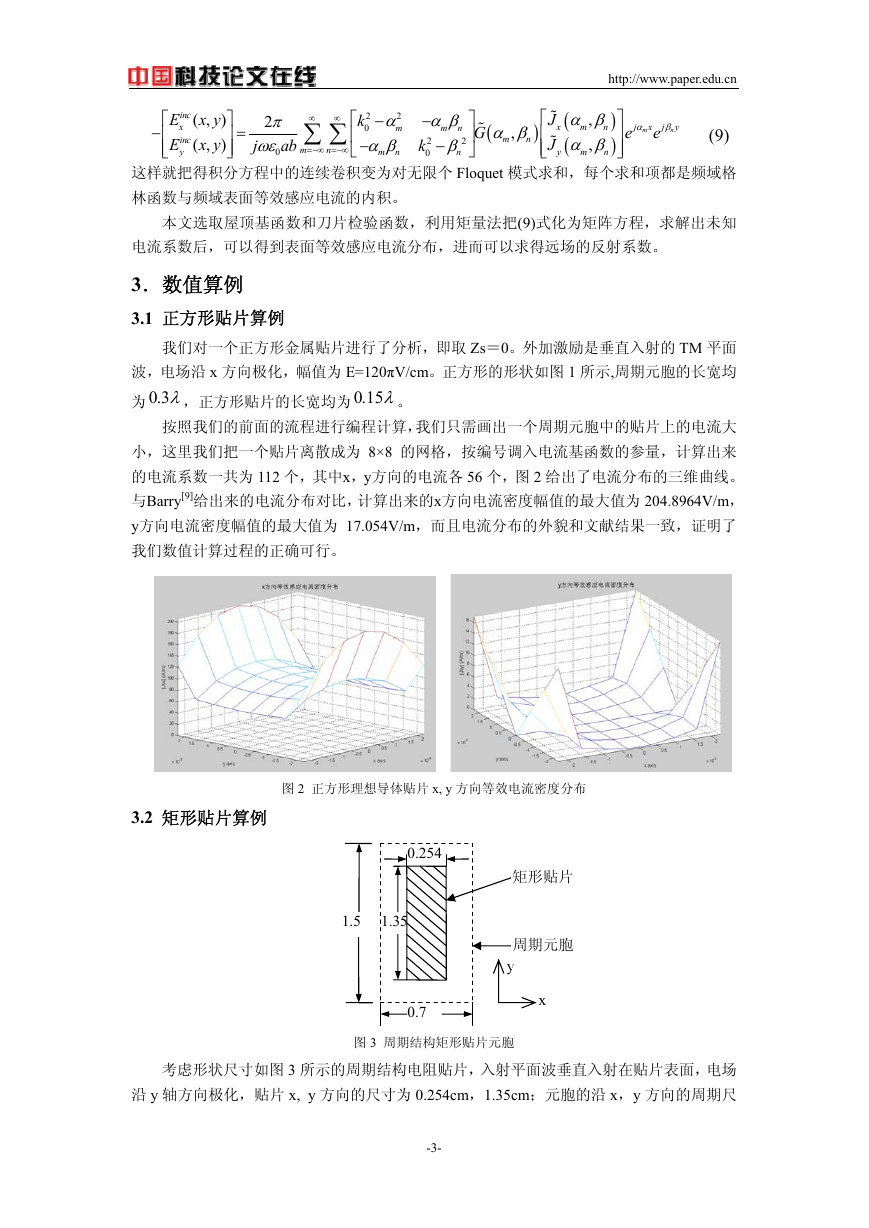
的电流系数一共为 112 个，其中x，y方向的电流各 56 个，图 2 给出了电流分布的三维曲线。
与Barry[9]给出来的电流分布对比，计算出来的x方向电流密度幅值的最大值为 204.8964V/m，
y方向电流密度幅值的最大值为 17.054V/m，而且电流分布的外貌和文献结果一致，证明了
我们数值计算过程的正确可行。
图 2 正方形理想导体贴片 x, y 方向等效电流密度分布
3.2 矩形贴片算例
0.254
1.5
1.35
矩形贴片
周期元胞
y
0.7
6
图 3 周期结构矩形贴片元胞
x
考虑形状尺寸如图 3 所示的周期结构电阻贴片，入射平面波垂直入射在贴片表面，电场
沿 y 轴方向极化，贴片 x, y 方向的尺寸为 0.254cm，1.35cm；元胞的沿 x，y 方向的周期尺
-3-
http://www.paper.edu.cn
寸为 0.76cm，1.52cm。每一个贴片 x 方向 Floquet 模式数取为 M＝30，y 方向 Floquet 模式
数为 N＝40，按照前面模式与网格划分的关系，我们一共需要计算 157 个表面等效感应电流，
其中 x 方向电流个数为 P＝72，y 方向电流个数为 Q＝85，我们首先观察一下贴片表面的电
流分布情况，如图 4 所示。这里取表面电阻 Zs=1Ω/□，垂直入射平面波电场沿 y 方向极化，
幅值为 Ey=377V/cm。
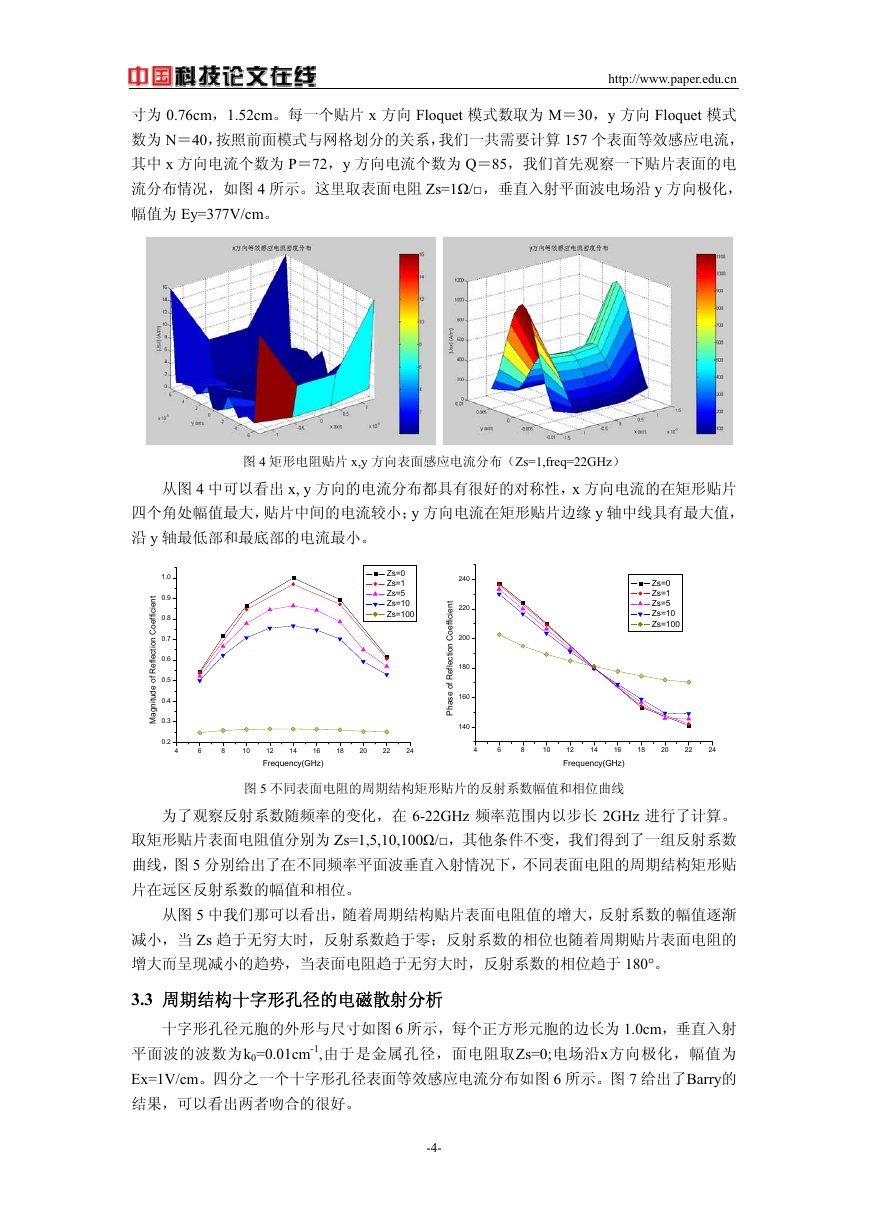
图 4 矩形电阻贴片 x,y 方向表面感应电流分布（Zs=1,freq=22GHz）
从图 4 中可以看出 x, y 方向的电流分布都具有很好的对称性，x 方向电流的在矩形贴片
四个角处幅值最大，贴片中间的电流较小；y 方向电流在矩形贴片边缘 y 轴中线具有最大值，
沿 y 轴最低部和最底部的电流最小。
t
i
n
e
c
i
f
f
e
o
C
n
o
i
t
c
e
l
f
e
R
f
o
e
d
u
t
i
n
g
a
M
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
Zs=0
Zs=1
Zs=5
Zs=10
Zs=100
t
i
n
e
c
i
f
f
e
o
C
n
o
i
t
c
e
l
f
e
R
f
o
4
6
8
10
14
12
16
Frequency(GHz)
18
20
22
24
e
s
a
h
P
Zs=0
Zs=1
Zs=5
Zs=10
Zs=100
240
220
200
180
160
140
4
6
8
10
14
12
16
Frequency(GHz)
18
20
22
24
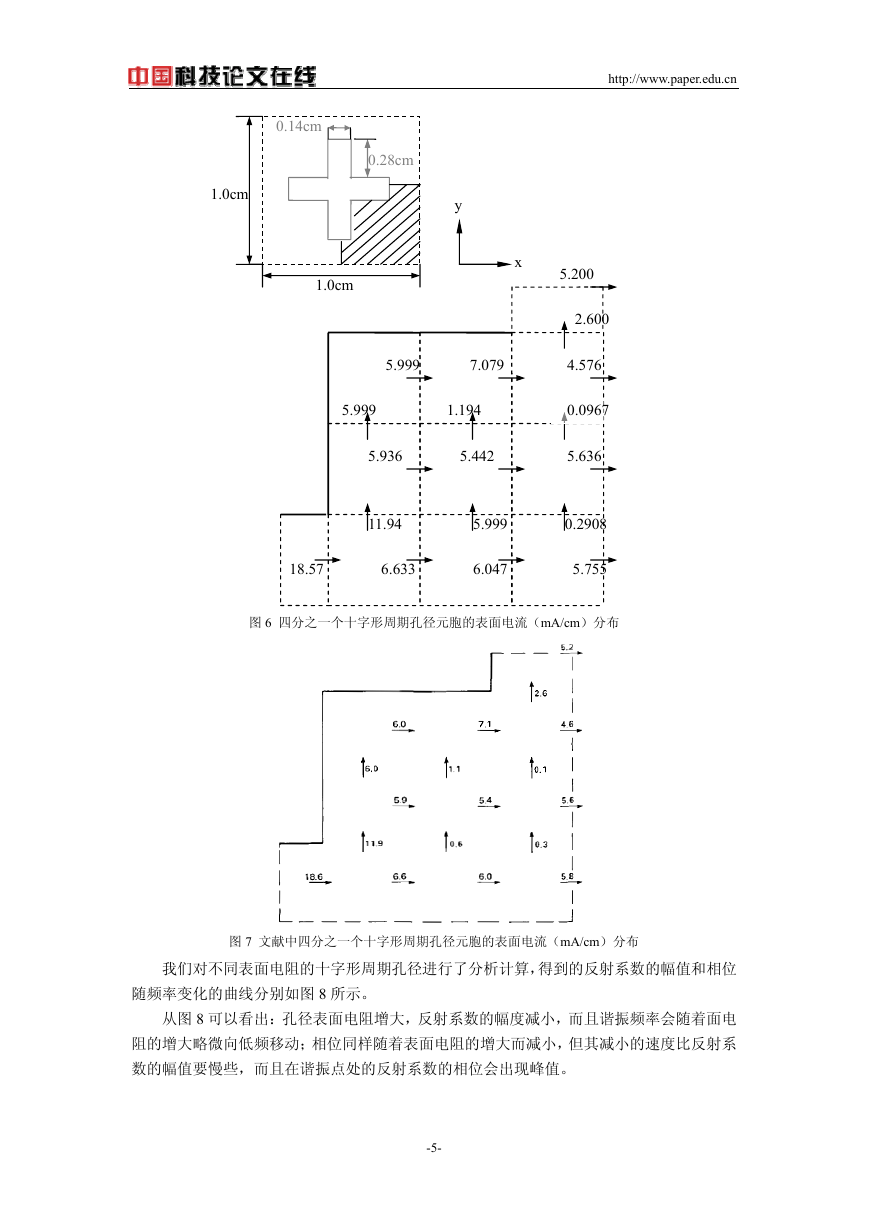
图 5 不同表面电阻的周期结构矩形贴片的反射系数幅值和相位曲线
为了观察反射系数随频率的变化，在 6-22GHz 频率范围内以步长 2GHz 进行了计算。
取矩形贴片表面电阻值分别为 Zs=1,5,10,100Ω/□，其他条件不变，我们得到了一组反射系数
曲线，图 5 分别给出了在不同频率平面波垂直入射情况下，不同表面电阻的周期结构矩形贴
片在远区反射系数的幅值和相位。
从图 5 中我们那可以看出，随着周期结构贴片表面电阻值的增大，反射系数的幅值逐渐
减小，当 Zs 趋于无穷大时，反射系数趋于零；反射系数的相位也随着周期贴片表面电阻的
增大而呈现减小的趋势，当表面电阻趋于无穷大时，反射系数的相位趋于 180°。
3.3 周期结构十字形孔径的电磁散射分析
十字形孔径元胞的外形与尺寸如图 6 所示，每个正方形元胞的边长为 1.0cm，垂直入射
平面波的波数为k =0.01cm-1
,由于是金属孔径，面电阻取Zs=0;电场沿x方向极化，幅值为
Ex=1V/cm。四分之一个十字形孔径表面等效感应电流分布如图 6 所示。图 7 给出了Barry的
结果，可以看出两者吻合的很好。
0
-4-
http://www.paper.edu.cn
0.14cm
1.0cm
0.28cm
y
1.0cm
x
5.200
2.600
5.999
7.079
4.576
5.999
1.194
5.936
5.442
11.94
18.57
6.633
5.999
6.047
0.0967
5.636
0.2908
5.755
图 6 四分之一个十字形周期孔径元胞的表面电流（mA/cm）分布
图 7 文献中四分之一个十字形周期孔径元胞的表面电流（mA/cm）分布
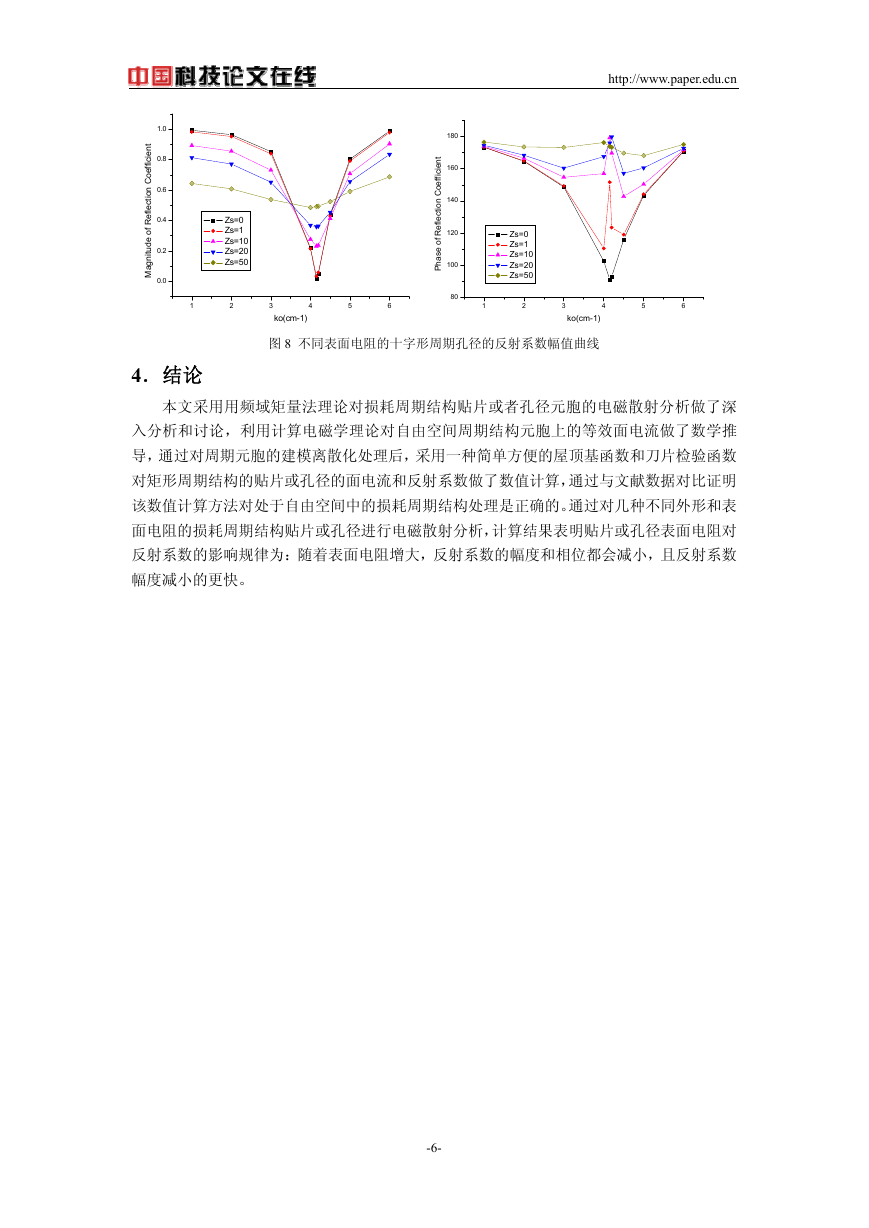
我们对不同表面电阻的十字形周期孔径进行了分析计算，得到的反射系数的幅值和相位
随频率变化的曲线分别如图 8 所示。
从图 8 可以看出：孔径表面电阻增大，反射系数的幅度减小，而且谐振频率会随着面电
阻的增大略微向低频移动；相位同样随着表面电阻的增大而减小，但其减小的速度比反射系
数的幅值要慢些，而且在谐振点处的反射系数的相位会出现峰值。
-5-
t
i
n
e
c
i
f
f
e
o
C
n
o
i
t
c
e
l
f
e
R
f
o
e
d
u
t
i
n
g
a
M
1.0
0.8
0.6
0.4
0.2
0.0
Zs=0
Zs=1
Zs=10
Zs=20
Zs=50
1
2
3
4
5
6
http://www.paper.edu.cn
180
160
140
120
100
80
Zs=0
Zs=1
Zs=10
Zs=20
Zs=50
1
2
3
4
5
6
t
i
n
e
c
i
f
f
e
o
C
n
o
i
t
c
e
l
f
e
R
f
o
e
s
a
h
P
ko(cm-1)
ko(cm-1)
图 8 不同表面电阻的十字形周期孔径的反射系数幅值曲线
4．结论
本文采用用频域矩量法理论对损耗周期结构贴片或者孔径元胞的电磁散射分析做了深
入分析和讨论，利用计算电磁学理论对自由空间周期结构元胞上的等效面电流做了数学推
导，通过对周期元胞的建模离散化处理后，采用一种简单方便的屋顶基函数和刀片检验函数
对矩形周期结构的贴片或孔径的面电流和反射系数做了数值计算，通过与文献数据对比证明
该数值计算方法对处于自由空间中的损耗周期结构处理是正确的。通过对几种不同外形和表
面电阻的损耗周期结构贴片或孔径进行电磁散射分析，计算结果表明贴片或孔径表面电阻对
反射系数的影响规律为：随着表面电阻增大，反射系数的幅度和相位都会减小，且反射系数
幅度减小的更快。
-6-
http://www.paper.edu.cn
参考文献
[1] B.A. Munk Frequency Selective Surfaces: Theory and Design New York:Wiley, 2000.
[2] E.Yablonovitch, “Inhibited spontaneous emission in solid-state physics and electronics,” Phys. Rev. Lett ,
1987, 58:2059-2062
[3] V.G. Vesalago. The electrodynamics of substances with simultaneously negative value of εandμ,Sov. Phys.
Usp.1968,10(4):509-514
[4] 陈良,等. 电阻贴片频率选择表面（FSSR）的吸波性能研究.电波科学学报.2006.8
[5] 刘红英,等. 利用频率选择表面改善微波吸收材料 S 波段的吸波性能.微波学报 2006.6
[6] Wei Bing Lu, Tie Jun Cui. Accurate Analysis of Large-Scale Periodic Structures Using an Efficient Sub-
Entire -Domain Basis Function Method. IEEE Transactions on Anttennas and Propagation. 2004,52(11):3078-3085
[7] 周永江,等. 十字型电阻贴片频率选择表面吸收体吸波性能研究. 材料工程. 2006.增刊 1
[8] 马嘉俊,等. 介质频率选择表面 FDTD 法分析. 陕西工学院学报.2004.12
[9] T.K.WU. Frequency selective surface and grid array. A Wiley-Intersceince publication. 1995:27-49
[10] Brray.J.Rubin, Henry L.Bertoni. Reflection from a perforated plane using a subsectional current approxima
tion. IEEE Transactions on Antennas and Propagation 1983, 31(6):829-836
Analysis of Electromagnetic Scattering from Freestanding
Periodic Structures Patches/Apertures
State Key Laboratory of Electronic Thin Films and integrated Devices, University of Electronic
Meng Lin
Science and Technology, Chengdu, PRC (610054)
Email: tomclus006@163.com
Abstract
In this paper, the method of moments in spectral domain is used to analyze electromagnetic scattering
of free lossy periodic structures patches or apertures. The equivalent surface current distribution and
reflection coefficient are calculated. The numerical results are compared with the reference and
discussed.
Key words: lossy periodic structures, electro-magnetic scattering, methods of moment in spectral
domain, equivalent surface currents, reflection coefficient
-7-
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
