无源 RC 滤波器设计性学生实验方案构思 钟建 于军胜 蒋泉 陶斯禄 张磊 林慧 电子科技大学光电信息学院（四川 成都 610054） 摘 要: 滤波器是一种能使有用信号顺利通过而同时对无用频率信号进行抑制（或衰减）的 电子装置。工程上常用它来做信号处理、数据传送和抑制干扰等。本实验方案主要是针对由 R、C 组成的无源滤波器进行介绍，对各种无源 RC 滤波器的幅频特性和相频特性进行分析。 然后对转折频率 ωC =1000rad/s 的情形分别提出一个一阶 RC 无源低、高通滤波器和一个二 阶 RC 无源低通滤波器的学生实验设计方案，对所设计的方案进行频率特性的研究。 关键词: 无源 RC 滤波器设计 实验方案 中图分类号: 153 文献标识码: Ａ 文章编号: 一、前沿 随着电力电子技术的迅速发展，特别是在冶金、矿山、电气化铁道、电力输送等工业系 统中大量采用可控硅技术及其硅整流设备和换流逆变设备，这些非线性负荷在系统中产生大 量谐波，从而影响了电能质量并导致经济损失。现在虽然提出了有源滤波器等技术来抑制谐 波，但由于有源滤波器容量较小，成本较高，因此实际工程应用中大多数仍然采用技术较为 成熟的无源滤波器，相对来说无源滤波器价格便宜，容易实现。因此在这些领域中，信号频 率相对来说不高。无源 RC 滤波器是很容易设计的，并且它们不需要外部直流激励[1]。对无 源 RC 低/高通滤波器的测试表明，它们的响应曲线是单调的。利用合适的元件滤波器，相关 止带部分的能量衰减度超过 40dB。通过选用最小数量的不同值元件来降低成本是有可能的。 总之，无源 RC 滤波器对高电压和高功率应用来说是一个很好的设计选择。RC 滤波器电路简 单，抗干扰性强，有较好的低频性能，并且选用标准的阻容元件易得，所以在工程测试的领 域中最经常用到的滤波器是 RC 滤波器[2]。对各种无源 RC 滤波器的滤波特性做简要的分析， 并提出一些设计方案，对所设计的方案进行频率特性的研究。 无源滤波器通常是以 L-C、R-C 等无源器件组成的一种只允许通过给定的频带信号而阻 止其它频率信号通过的选频网络。无源滤波器常用在旁路、平滑滤波、电源去耦以及高频 滤波等电路中。在测试系统中，常用 RC 滤波器。因为在这一领域中，信号频率相对来说不 

高。而 RC 滤波器电路简单，抗干扰性强，有较好的低频性能，并且选用标准的阻容元件易 得，所以在工程测试的领域中最经常用到的滤波器是 RC 滤波器[3]。对各种无源 RC 滤波器的 滤波特性做简要的分析，并提出一些设计方案，对所设计的方案进行频率特性的研究。 二、 一阶 RC 低通滤波器实验方案[4] 一阶 RC 低通滤波电路采用 RC 串联电路，把 R 或 C 做为负载端，对负载端与输入端的信 号做比较得到电路的特性曲线。图 1 所示 RC 串联电路构成一个双口网络， 图 1 一阶 RC 低通滤波的实验电路图 根据图 1，其负载端开路时电容电压对输入电压的转移电压比为 H j( ) ω = U & U & 2 1 = R 1 C j ω 1 C j ω + = 1 j1 ω + RC 这是一个典型的一阶系统。 分析可知，当 ω 很小时， j( ωH ) =1，信号不受衰减的通过；当 f 很大时， j( ωH ) =0， 信号完全被阻挡，不能通过。利用 MATLAB 工具描绘一阶 RC 无源低通滤波器幅频特性曲 线和相频特性曲线如图 2 所示。 图 2 一阶 RC 低通滤波的幅频与相频特性曲线 三、 一阶 RC 高通滤波器实验方案 一阶 RC 高通滤波电路采用 RC 串联电路，把 R 或 C 做为负载端，对负载端与输入 端的信号做比较[5]，得到电路的特性曲线。图 3 所示 RC 串联电路构成一个双口网络， 

图 2 一阶 RC 高通滤波电路图 根据图 3，根据分析可得电阻电压对输入电压的转移电压比为： H j( ) ω = U & U & 2 1 = R 1 C j ω R + = RC j ω RC j1 ω + 分析可知，当 f 很小时，A(f)=0，信号完全被阻挡，不能通过；当 f 很大时，A(f)=1 信号不受衰减的通过。设计 ωC =100rad/s 的一阶 RC 高通滤波器的电路如下图所示，其 中 R=100Ω，C=1μF，利用 MATLAB 工具可描绘一阶 RC 无源高通滤波器幅频特性曲线和相 频特性曲线。 四、 二阶 RC 低通滤波器实验方案 与一阶 RC 滤波电路相比，二阶 RC 由 R、C 串并联而成，结构上稍显复杂，同时 二阶 RC 电路对同频带外信号的抑制能力更强，滤波效果更好[6]。二阶 RC 滤波电路不仅 能实现低通和高通滤波特性，还能实现带通滤波特性。其具体实验方案如图 4： 图 4 二阶 RC 低通滤波电路图 由分析可知电容电压对输入电压的转移电压比为： H j( ) ω = U & U & 2 1 = 1 CR 2 2 1 − 2 ω = + j3 ω RC jH ( ) ) ωθω ∠ ( ，其中： 

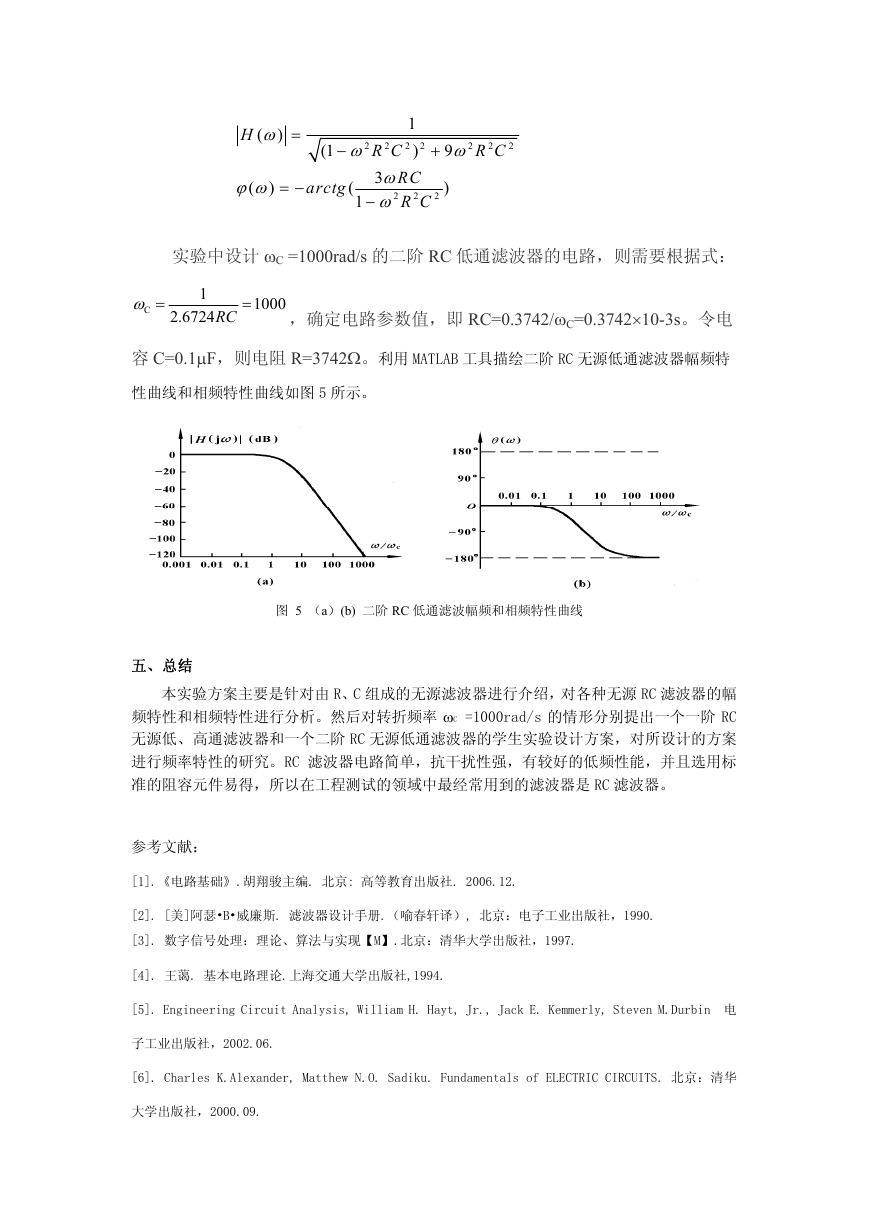
H ( ) ω = (1 − 2 ω ) ϕω ( = − arctg ( 1 2 1 R C ) 2 RC 3 ω R C 2 2 − ω ) 2 2 + 9 2 ω 2 R C 2 实验中设计 ωC =1000rad/s 的二阶 RC 低通滤波器的电路，则需要根据式： ω C = 1 6724 .2 RC = 1000 ，确定电路参数值，即 RC=0.3742/ωC=0.3742×10-3s。令电 容 C=0.1μF，则电阻 R=3742Ω。利用 MATLAB 工具描绘二阶 RC 无源低通滤波器幅频特 性曲线和相频特性曲线如图 5 所示。 五、总结 图 5 （a）(b) 二阶 RC 低通滤波幅频和相频特性曲线 本实验方案主要是针对由 R、C 组成的无源滤波器进行介绍，对各种无源 RC 滤波器的幅 频特性和相频特性进行分析。然后对转折频率 ωC =1000rad/s 的情形分别提出一个一阶 RC 无源低、高通滤波器和一个二阶 RC 无源低通滤波器的学生实验设计方案，对所设计的方案 进行频率特性的研究。RC 滤波器电路简单，抗干扰性强，有较好的低频性能，并且选用标 准的阻容元件易得，所以在工程测试的领域中最经常用到的滤波器是 RC 滤波器。 参考文献： [1].《电路基础》.胡翔骏主编. 北京: 高等教育出版社. 2006.12. [2]. [美]阿瑟•B•威廉斯. 滤波器设计手册.（喻春轩译）, 北京：电子工业出版社，1990. [3]. 数字信号处理：理论、算法与实现【M】.北京：清华大学出版社，1997. [4]. 王蔼. 基本电路理论.上海交通大学出版社,1994. [5]. Engineering Circuit Analysis, William H. Hayt, Jr., Jack E. Kemmerly, Steven M.Durbin 电 子工业出版社，2002.06. [6]. Charles K.Alexander, Matthew N.O. Sadiku. Fundamentals of ELECTRIC CIRCUITS. 北京：清华 大学出版社，2000.09.