支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版

第1页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第2页.png

第2页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第3页.png

第3页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第4页.png

第4页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第5页.png

第5页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第6页.png

第6页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第7页.png

第7页 / 共52页

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf-第8页.png

第8页 / 共52页

支持向量机通俗导论理解 SVM 的三层境界作者： July 致谢： pluskid、白石、JerryLead 出处：结构之法算法之道 blog

目录目录 1 第一层：了解 SVM 1.1 分类标准的起源：Logistic 回归 . . . . . . . . . . . . . . . . . . . . . . . . 1.2 线性分类的一个例子 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.3 函数间隔 Functional margin 与几何间隔 Geometrical margin . . . . . . . 1.4 最大间隔分类器 Maximum Margin Classiﬁer 的定义 . . . . . . . . . . . . 2 4 4 5 8 9 2 第二层：深入 SVM 12 2.1 从线性可分到线性不可分 . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.1.1 从原始问题到对偶问题的求解 . . . . . . . . . . . . . . . . . . . . . 12 2.1.2 K.K.T. 条件 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.1.3 对偶问题求解的 3 个步骤 . . . . . . . . . . . . . . . . . . . . . . . 14 2.1.4 线性不可分的情况 . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 2.2 核函数：Kernel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.2.1 特征空间的隐式映射：核函数 . . . . . . . . . . . . . . . . . . . . . 18 2.2.2 核函数：如何处理非线性数据 . . . . . . . . . . . . . . . . . . . . . 19 2.2.3 几个核函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.2.4 核函数的本质 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 2.3 使用松弛变量处理 outliers 方法 . . . . . . . . . . . . . . . . . . . . . . . . 24 3 证明 SVM 29 3.1 线性学习器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 3.1.1 感知器算法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 3.2 非线性学习器 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 3.2.1 Mercer 定理 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 3.3 损失函数 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 3.4 最小二乘法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 3.4.1 什么是最小二乘法？ . . . . . . . . . . . . . . . . . . . . . . . . . . 34 3.4.2 最小二乘法的解法 . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 3.5 SMO 算法 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 SMO 算法的推导 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 SMO 算法的步骤 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 SMO 算法的实现 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 3.6 SVM 的应用 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 3.6.1 文本分类 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 3.5.1 3.5.2 3.5.3

目录 3 前言动笔写这个支持向量机 (Support Vector Machine1) 是费了不少劲和困难的，原因很简单，一者这个东西本身就并不好懂，要深入学习和研究下去需花费不少时间和精力，二者这个东西也不好讲清楚，尽管网上已经有朋友写得不错了 (见文末参考链接)，但在描述数学公式的时候还是显得不够。得益于同学白石的数学证明，我还是想尝试写一下，希望本文在兼顾通俗易懂的基础上，真真正正能足以成为一篇完整概括和介绍支持向量机的导论性的文章。本文在写的过程中，参考了不少资料，包括《支持向量机导论》、《统计学习方法》及网友 pluskid 的支持向量机系列等等，于此，还是一篇学习笔记，只是加入了自己的理解和总结，有任何不妥之处，还望海涵。全文宏观上整体认识支持向量机的概念和用处，微观上深究部分定理的来龙去脉，证明及原理细节，力保逻辑清晰 & 通俗易懂。同时，阅读本文时建议大家尽量使用 chrome 等浏览器，如此公式才能更好的显示，再者，阅读时可拿张纸和笔出来，把本文所有定理. 公式都亲自推导一遍或者直接打印下来（可直接打印网页版或本文文末附的 PDF，享受随时随地思考、演算的极致快感），在文稿上演算。 OKL，还是那句原话，有任何问题，欢迎任何人随时不吝指正 & 赐教，感谢。 1http://en.wikipedia.org/wiki/Support_vector_machine

1 第一层：了解 SVM 4 1 第一层：了解 SVM 支持向量机，因其英文名为 Support Vector Machine，故一般简称 SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。 1.1 分类标准的起源：Logistic 回归理解 SVM，咱们必须先弄清楚一个概念：线性分类器。给定一些数据点，它们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。如果用 x 表示数据点，用 y 表示类别（y 可以取 1 或者 1，分别代表两个不同的类），一个线性分类器的学习目标便是要在 n 维的数据空间中找到一个超平面（hyper plane），这个超平面的方程可以表示为（wT 中的 T 代表转置）： (1.1) 可能有读者对类别取 1 或 1 有疑问，事实上，这个 1 或 1 的分类标准起源于 wT x + b = 0 Logistic 回归2。定义 1 (Logistic 回归) Logistic 回归目的是从特征学习出一个 0/1 分类模型，而这个模型是将特征的线性组合作为自变量，由于自变量的取值范围是负无穷到正无穷，因此，使用 Logistic 函数（或称作 sigmoid 函数）将自变量映射到 (0; 1) 上，映射后的值被认为是属于 y = 1 的概率。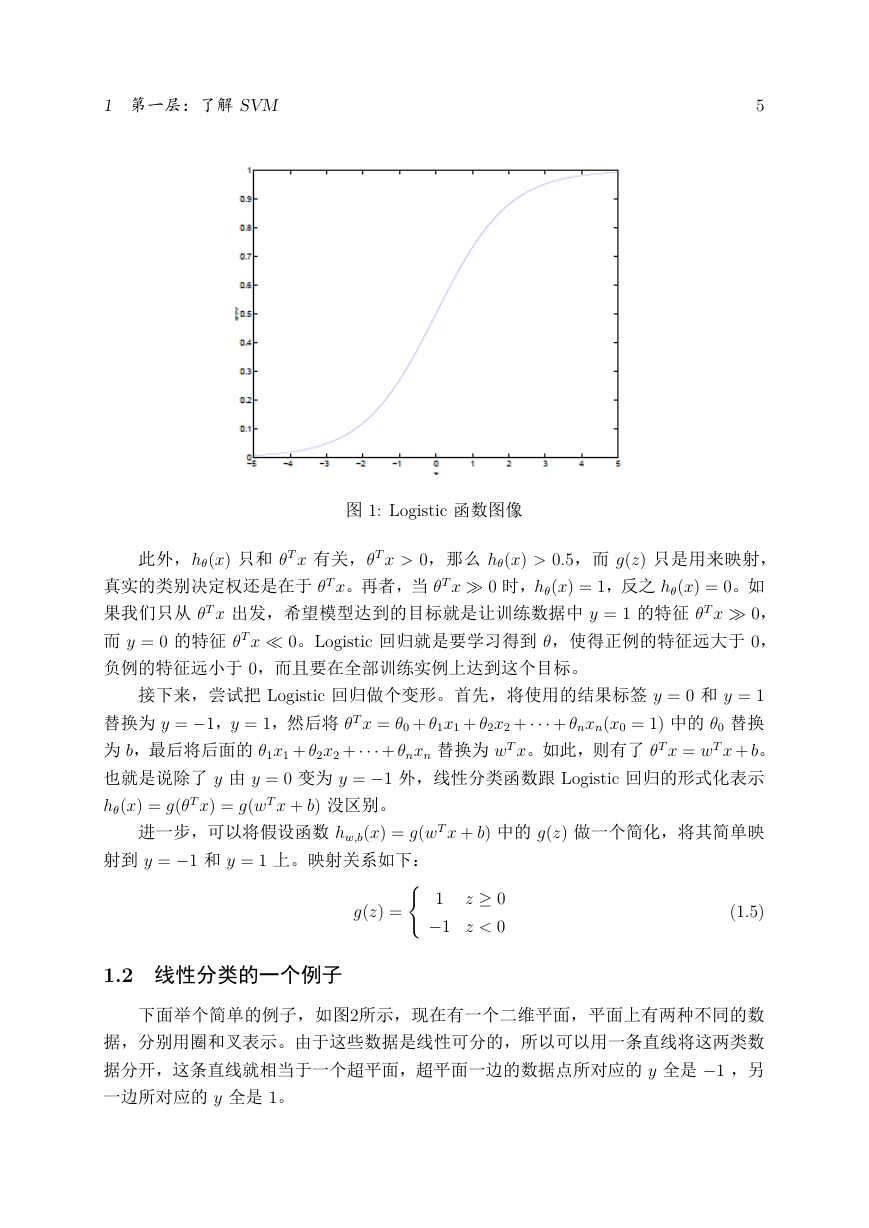假设函数: h(x) = g(T x) = 1 1 + eT x (1.2) 其中，x 是 n 维特征向量，函数 g 就是 Logistic 函数。而 g(z) = 1 1+ez 的图像如图1，将无穷映射到了 (0; 1)。而假设函数就是属于 y = 1 的概率： P (y = 1jx; ) = h(x) P (y = 0jx; ) = 1 h(x) (1.3) (1.4) 从而，当我们要判别一个新来的特征属于哪个类时，只需求 h(x) 即可，若 h(x) 大于 0.5 就是 y = 1 的类，反之属于 y = 0 类。 2http://en.wikipedia.org/wiki/Logistic_regression

1 第一层：了解 SVM 5 图 1: Logistic 函数图像此外，h(x) 只和 T x 有关，T x > 0，那么 h(x) > 0:5，而 g(z) 只是用来映射，真实的类别决定权还是在于 T x。再者，当 T x ≫ 0 时，h(x) = 1，反之 h(x) = 0。如果我们只从 T x 出发，希望模型达到的目标就是让训练数据中 y = 1 的特征 T x ≫ 0，而 y = 0 的特征 T x ≪ 0。Logistic 回归就是要学习得到，使得正例的特征远大于 0，负例的特征远小于 0，而且要在全部训练实例上达到这个目标。接下来，尝试把 Logistic 回归做个变形。首先，将使用的结果标签 y = 0 和 y = 1 替换为 y = 1，y = 1，然后将 T x = 0 + 1x1 + 2x2 + + nxn(x0 = 1) 中的 0 替换为 b，最后将后面的 1x1 + 2x2 + + nxn 替换为 wT x。如此，则有了 T x = wT x + b。也就是说除了 y 由 y = 0 变为 y = 1 外，线性分类函数跟 Logistic 回归的形式化表示 h(x) = g(T x) = g(wT x + b) 没区别。进一步，可以将假设函数 hw;b(x) = g(wT x + b) 中的 g(z) 做一个简化，将其简单映 (1.5) { 射到 y = 1 和 y = 1 上。映射关系如下： g(z) = 1.2 线性分类的一个例子 z 0 1 1 z < 0 下面举个简单的例子，如图2所示，现在有一个二维平面，平面上有两种不同的数据，分别用圈和叉表示。由于这些数据是线性可分的，所以可以用一条直线将这两类数据分开，这条直线就相当于一个超平面，超平面一边的数据点所对应的 y 全是 1 ，另一边所对应的 y 全是 1。

1 第一层：了解 SVM 6 图 2: 线性分类示例这个超平面可以用分类函数 f (x) = wT x + b 表示，当 f (x) 等于 0 的时候，x 便是位于超平面上的点，而 f (x) 大于 0 的点对应 y = 1 的数据点，f (x) 小于 0 的点对应 y = 1 的点，如图3所示。图 3: 支持向量示例注 1 有的资料上定义特征到结果的输出函数 u = ⃗w⃗xb，与这里定义的 f (x) = wT x+b 实质是一样的。为什么？因为无论是 u = ⃗w ⃗x b，还是 f (x) = wT x + b，不影响最终优 yi(wT xi + b) 1; i = 1; :::; n 化结果。下文你将看到，当我们转化到优化 max 1∥w∥ ; 的时候，为了求解方便，会把 yf (x) 令为 1，即 yf (x) 是 y(wT x + b)，还是 y(wT x b)，对我们要优化的式子 max 1∥w∥ 已无影响。 s:t: 注 2 有一朋友飞狗来自 Mare_Desiderii，看了上面的定义之后，问道：请教一下 SVM functional margin 为 ^ = y(wT x + b) = yf (x) 中的 y 是只取 1 和 -1 吗？y 的唯一作用就是确保 functional margin 的非负性？

1 第一层：了解 SVM 7 与白石讨论后，我来具体回答下这个问题：你把问题搞混了。y 是个分类标签，二分时 y 就取两个值，而刚好取了 -1 和 1，只是因为用超平面分类时，不同的类中的点函数值刚好有不同的符号，所以就用符号来进行分类。具体阐述如下： 1. 对于二类问题，因为 y 只取两个值，这两个是可以任意取的，只要是取两个值就行； 2. 支持向量机去求解二类问题，目标是求一个特征空间的超平面，而超平面分开的两类对应于超平面的函数值的符号是刚好相反的； 3. 基于上述两种考虑，为了使问题足够简单，我们取 y 的值为 1 和 -1； 4. 在取定分类标签 y 为 -1 和 1 之后，那么，一个平面正确分类样本数据，就相当于用这个平面计算的那个 y f (x) > 0； 5. 而且这样一来，y f (x) 有明确的几何含义；总而言之：你要明白，二类问题的标签 y 是可以取任意两个值的，不管取怎样的值对于相同的样本点，只要分类相同，所有的 y 的不同取值都是等价的，之所以取某些特殊的值，只是因为这样一来计算会变得方便，理解变得容易。正如朋友张磊所言，SVM 取 1 或 -1 的历史原因是因为感知器最初的定义，实际取值可以任意，总能明确表示输入样本是否被误分，但是用 +1、-1 可以起码可以是问题描述简单化、式子表示简洁化、几何意义明确化。举个例子，如你要是取 y 为 1 和 2，比如原来取 -1 的现在取 1，原来取 1 的现在取 2 ，这样一来，分类正确的判定标准变为 (y 1:5)f (x) > 0 ，故取 1 和 -1 只是为了计算简单方便，没有实质变化，更非一定必须取一正一负。当然，有些时候，或者说大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在 (不过关于如何处理这样的问题我们后面会讲)，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。换言之，在进行分类的时候，遇到一个新的数据点 x，将 x 代入 f (x) 中，如果 f (x) 小于 0 则将 x 的类别赋为 -1，如果 f (x) 大于 0 则将 x 的类别赋为 1。接下来的问题是，如何确定这个超平面呢？从直观上而言，这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以，得寻找有着最大间隔的超平面。

1 第一层：了解 SVM 8 1.3 函数间隔 Functional margin 与几何间隔 Geometrical margin 在超平面 wT x + b = 0 确定的情况下，jwT x + bj 能够表示点 x 到距离超平面的远近3，而通过观察 wT x + b 的符号与类标记 y 的符号是否一致可判断分类是否正确，所以，可以用 y(wT x + b) 的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。定义函数间隔（用 ^ 表示）为： ^ = y(wT x + b) = yf (x) (1.6) 而超平面 (w; b) 关于 T 中所有样本点 (xi; yi) 的函数间隔最小值（其中，x 是特征， y 是结果标签，i 表示第 i 个样本），便为超平面 (w; b) 关于训练数据集 T 的函数间隔： ^ = min ^i; (i = 1; :::; n) (1.7) 但这样定义的函数间隔有问题，即如果成比例的改变 w 和 b（如将它们改成 2w 和 2b），则函数间隔的值 f (x) 却变成了原来的 2 倍（虽然此时超平面没有改变），所以只有函数间隔还远远不够。事实上，我们可以对法向量 w 加些约束条件，从而引出真正定义点到超平面的距离——几何间隔（geometrical margin）的概念。假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个向量，为样本 x 到分类间隔的距离，如图4所示。图 4: 几何距离示例有 x = x0 + w∥w∥，其中 ∥w∥ 表示的是范数。又由于 x0 是超平面上的点，满足 f (x0) = 0 ，代入超平面的方程 wT x + b = 0 即可算出4： = wT x + b ∥w∥ = f (x)∥w∥ (1.8) 3整理者注：这里的“远近”是个相对概念，如果是计算点到超平面距离为：jwT x + bj/∥w∥ 4有的书上会写成把 ∥w∥ 分开相除的形式，如本文参考文献及推荐阅读条目《统计学习方法》，其中， ∥w∥ 为 w 的二阶范数

资料库

支持向量机通俗导论（理解SVM的三层境界）LaTeX最新版_2015.1.9.pdf

相关推荐

最新资料