智赢中考 ·AI逆袭智学卷
使用说明
第一步:专题测试---覆盖考点 全面测试
共××个专题
逐个专题进行过关测试
第二步:破习错题---错题轻松学 薄弱找准确
登录优鸿智学客户端,智能破习错题
轻松学会错题的同时,精准定位薄弱
第三步:查看学情---学情全知道 提分有方向
AI系统智能生成《学情分析报告》
精准了解学情、提分目标和方案
第四步:个性化学习---学习精准化 轻松就逆袭
AI系统一对一生成《个性化学案》
个性化精准学练,科学备考,精准提分
�
智赢中考·AI逆袭智学卷
专题五 二次函数
一、选择题
+
) 2
1 m m
x -
是关于 x 的二次函数,则 m 的值为(
).
m
1. 若 (
=
y
A. 2
2. 若直线 2
A. 第一象限
y
=
3. 把抛物线
y
= -
22
x
的函数关系式是(
)2
1
= -
x
(
A.
2
y
-
+
B.
1-
C.
x m
- 经过第一、三、四象限,则抛物线
1- 或 2
2(
y
=
D. 其它都不对
x m
+
)
2
- 的顶点必在( ).
1
+
4
B. 第二象限
+ 向左平移 2 个单位长度,再向上平移3 个单位长度,所得的抛物线
1
x
).
C. 第三象限
D. 第四象限
6
B.
y
= -
2
x
(
-
)2
1
-
C.
y
= -
2
+
x
(
y
+
6
)2
1
(
a x m x m k
)(
-
-
-
D.
)2
1
a > , ,m k 是实数),则(
= -
x
(
2
0
y
+
-
)
(
=
4. 设二次函数
A. 当 2
B. 当 2
C. 当 4
D. 当 4
k = 时,函数 y 的最小值为 a-
k = 时,函数 y 的最小值为 2a-
k = 时,函数 y 的最小值为 a-
k = 时,函数 y 的最小值为 2a-
6
6
).
5. 已知二次函数
y
=
2
x m
- 的图象与一次函数 2
= 的图象有两个交点,则 m 的取值范围是
y
x
(
).
1
6. 一次函数 y
m > -
A.
B.
0m
C.
=
ax
+ 的图象如图所示,则二次函数
b
m < -
2
ax
=
y
2
+ 的图象可能是(
D.
bx
0m <
).
A.
B.
C.
D.
二、填空题
7. 如图是二次函数
y
=
2
ax
+
bx
+ 图象的一部分,其对称轴为直线 1
x = ,若其与 x 轴的一交点为
c
(3 ),0A ,则由图象可知,不等式 2
ax
+
bx
+
c
> 的解集是
0
.
1
�
智赢中考·AI逆袭智学卷
8. 如图是二次函数
abc < ;② 2
0
2
+
y
bx
=
= ;③ 4
a b-
ax
0
c
+
+ 的图象的一部分,其对称轴为
(3,
a
< ;④若
( 6,
-
2
b
0
c
+
)y
1
, 2
1
x = - ,且过点 ( 4,0)
.①
)y 是抛物线上两点,则 1
y
A -
y>
.
2
其中结论正确的是________.
9. 若关于 x 的一元二次方程 (
x
-
2)(
x
-
3)
= 有实数根 1x 、 2x ,且 1
x
m
x¹
2
x
.① 1
=
2 ,
x
2
= ;②
3
m > - ;③二次函数
1
4
y
=
(
x
-
x
1
)(
x
-
x
2
)
+ 的图象与 x 轴交点的坐标为 (2,0) 和 (3,0) .其中正
m
确结论的个数是________.
10. 如图,把抛物线
y
=
21
x
2
平移得到抛物线 m ,抛物线 m 经过点 ( 8,0)
A -
和原点 (0,0)
O
,它的顶
点为 P ,它的对称轴与抛物线
y
=
21
x
2
交于点Q ,则图中阴影部分的面积为
.
11. 抛物线
y
=
2
ax
+
bx
+ ( ,
,a b c 是常数, 0
c < )经过( )1,1 ,(
c
),0m ,( ),0n 三点,且 3n
.
下列四个结论:
① 0
b < ;
2
4
ac b
②
-
③当 3
n = 时,若点( )2,t 在该抛物线上,则 1
< ;
4
a
t > ;
④若关于 x 的一元二次方程 2ax
+
bx
+
c
= 有两个相等的实数根,则
x
0
<
m
其中正确的是________(填序号).
1
3
.
2
�
智赢中考·AI逆袭智学卷
12. 已知关于 x 的一元二次方程
2
x
-
4
x
+
2
k
(
-
1
)
= 有两个不相等的实数根.
0
(1) k 的取值范围为
(2) 当 k 取最大整数时,抛物线
x 轴的交点坐标为
(3) 将(2)中求得的抛物线在 x 轴下方的部分沿 x 轴翻折到 x 轴的上方,图象的其他部分不变,
得到一个新图象,新图象与直线 y
x m
+ 有三个不同的公共点时 m 的值为
;
x
;
- 的顶点坐标为
,抛物线与
2(
k
1)
4
x
y
.
=
-
=
2
+
三、解答题
13. 如图,已知二次函数
+
=
y
bx
21
x
2
(1) 求二次函数的解析式;
(2) 抛物线的顶点为点 B ,连接 BD ,求 BD 的长;
(3) 在同一坐标系中画出直线
+ 与 x 轴交于 (2,0)
A
c
, ( 1,0)
D -
两点.
y
x=
+ ,并写出当 x 在什么范围内时,一次函数的值大于二次
1
函数的值.
14. 某旅行社有 120 张床位,每床每晚收费 20 元时,床位可全部租出,若每床每晚收费提高 2 元,
则减少 10 张床位的租出;若每床每晚收费再提高 2 元,则再减少 10 张床位租出,以每次提高
2 元的这种方法变化下去,为了投资少而获利大,每床每晚应提高多少元?
15. 话说孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞进行改造翻新.
计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺
就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达3 米,落在地上时距离喷水管 6
米,如图所示,问小道的边缘距离喷水管至少应为多少米,才能使身高不大于 1.92 米的游客
进入水帘洞时不会被水淋湿?
16. 王强在一次高尔夫球的练习中,在某处击球,球飞行的路线满足抛物线
y
= -
21
x
5
+
16
5
x
,其
中 (m)
y 是球飞行的高度, (m)
x 是球飞出的水平距离,结果球离球洞的水平距离还有 4m .
3
�
智赢中考·AI逆袭智学卷
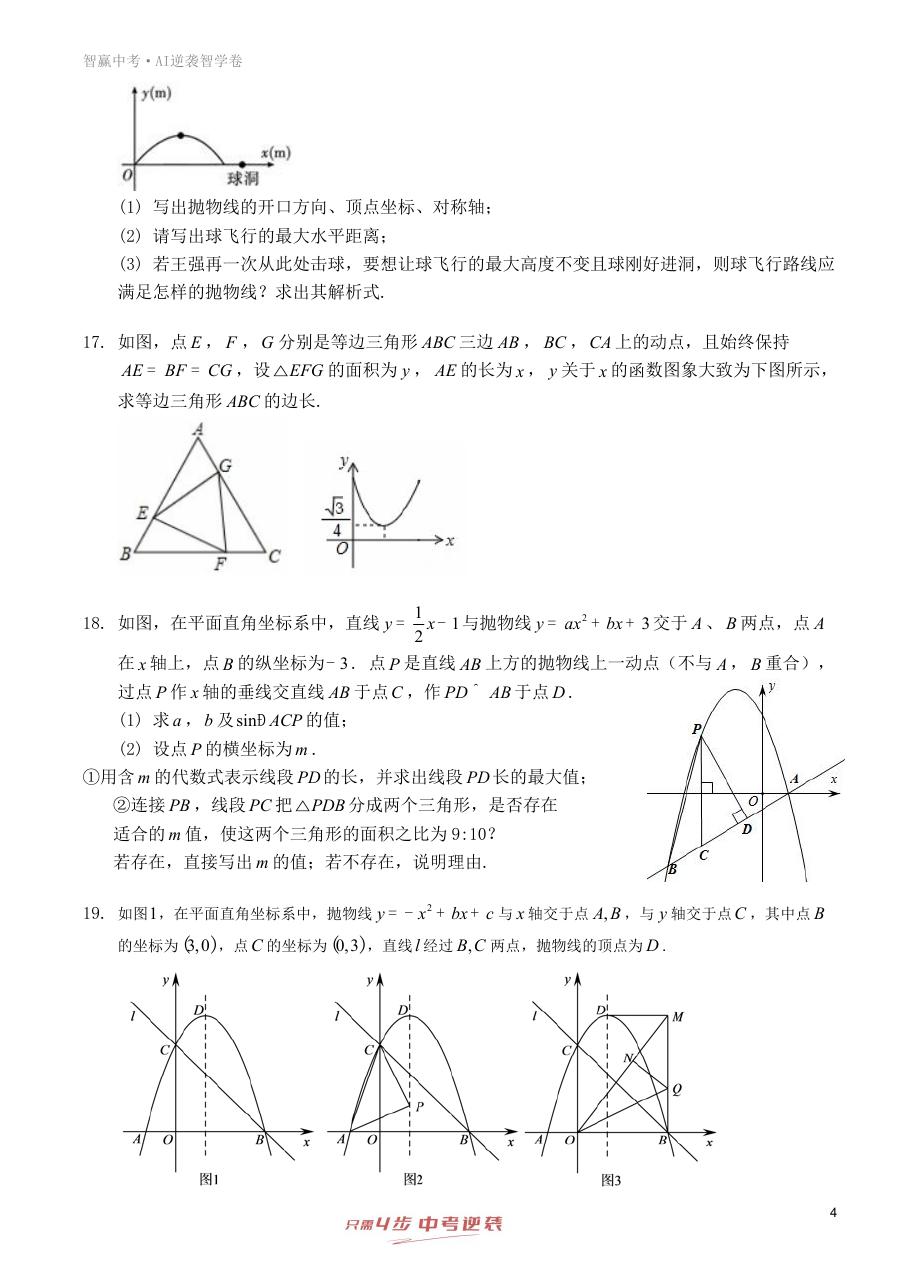
(1) 写出抛物线的开口方向、顶点坐标、对称轴;
(2) 请写出球飞行的最大水平距离;
(3) 若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应
满足怎样的抛物线?求出其解析式.
17. 如图,点 E , F ,G 分别是等边三角形 ABC 三边 AB , BC ,CA 上的动点,且始终保持
=
=
BF CG
,设 EFG△
AE
求等边三角形 ABC 的边长.
的面积为 y , AE 的长为 x , y 关于 x 的函数图象大致为下图所示,
18. 如图,在平面直角坐标系中,直线 1
2
y
=
x
- 与抛物线
1
y
=
2
ax
+
bx
+ 交于 A 、 B 两点,点 A
3
在 x 轴上,点 B 的纵坐标为 3- . 点 P 是直线 AB 上方的抛物线上一动点(不与 A , B 重合),
过点 P 作 x 轴的垂线交直线 AB 于点C ,作 PD AB^ 于点 D .
(1) 求 a ,b 及sin ACP
(2) 设点 P 的横坐标为 m .
的值;
Ð
①用含 m 的代数式表示线段 PD 的长,并求出线段 PD 长的最大值;
②连接 PB ,线段 PC 把 PDB△
适合的 m 值,使这两个三角形的面积之比为 9:10?
若存在,直接写出 m 的值;若不存在,说明理由.
分成两个三角形,是否存在
19. 如图1,在平面直角坐标系中,抛物线
y
= -
2
x
+
bx
+ 与 x 轴交于点 ,A B ,与 y 轴交于点C ,其中点 B
c
的坐标为( )3,0 ,点 C 的坐标为( )0,3 ,直线l 经过 ,B C 两点,抛物线的顶点为 D .
4
�
智赢中考·AI逆袭智学卷
(1) 求抛物线和直线l 的解析式;
(2) 如图 2 ,点 P 是抛物线对称轴上一动点,若以点 ,
P 的坐标;
(3) 如图3 ,过点 D 作 x 轴的平行线,过点 B 作 y 轴的平行线,两平行线交于点 M ,连接OM .点Q 是线
段 MB 上一动点,在线段OM 上是否存在这样的点 N ,使 NOQ△
形?若存在,请直接写出点 N 的坐标;若不存在,请说明理由.
,P A C 为顶点的三角形是等腰三角形,求出此时点
为等腰三角形且 NMQ△
为直角三角
20. 在平面直角坐标系中,已知抛物线经过 ( 4,0)
A -
, (0, 4)
B - , (2,0)
C
三点.
(1) 求抛物线的解析式;
(2) 若点 M 为第三象限内抛物线上一动点,点 M 的横坐标为 m , AMB△
数关系式,并求出 S 的最大值;
(3) 若点 P 是抛物线上的动点,点Q 是直线 y
的四边形为平行四边形,写出相应的点Q 的坐标.
x
= - 上的动点,判断有几个位置能使以点 ,
P Q B O 为顶点
,
的面积为 S .求 S 关于 m 的函
,
优鸿智学客户端
【客户端下载】平板和手机在应用商店搜索“优鸿智学”客户端下载,推荐使用平板,学习体验更优;
【注册激活】注册时输入专题激活码激活专题;
【智能学习】在优鸿智学客户端破习错题、查看学情分析、个性化学练。
5
�